Predicting Go players' strength with Convolutional Neural Nets
Ok, as this is my first blog-post here, so I should probably say why did I start. I want to use this platform to share what I do and maybe get some feedback for my work as well (I am working on comments, until then, e-mails are most welcome).
Introduction
Now about the actual subject. As probably everyone around nowadays, I’ve been toying with deep learning recently. The domain of my interest is computer Go and since the Go board is essentially a 19x19 bitmap with spatial properties, convolutional neural nets are clear choice. Most researchers in computer Go are trying to make strong computer programs (which is a hard problem). Making strong programs means knowing what is the strongest move in a given position, which makes for simple translation to the language of convolutional networks. Since we also have a lot of Go game records around, we have some ideas for research papers and fun.
Obviously, this idea has been around for some time now, but recently it has started to be really hot; see [Clark, Storkey 2014] and [Maddison et al. 2015] for starters. Just recently, a paper from FB research [Tian, Zhu 2015] has made a great deal of hype in the news, improving on the previous results. However the FB really seems to have some people working on this hard, as their bot combining the Monte Carlo Tree Search (prevalent technology in strong bots nowadays) with the CNN priors ended up third on the first tournament it played. Moreover it lost on time in both games, so lets see if they can actually win once they improve the time management.
Strength Prediction
In the past, I’ve been working on predicting Go player’s strength and playing style (Gostyle Project), so I wanted to try how good are CNN’s there. The idea is to give the network a position and teach it what are the players’ strengths instead of predicting the good move. In Go the strength is measured in kyu/dan ranks; for us, imagine we have a scale of — say — 24 ranks. The ranks have ordering (rank 1 is stronger player than rank 2), so regression seems like a good choice to begin the experiments with.
Dataset
I used some 71,119 games from the KGS Archives. Each game has on average circa 190 moves, so in the end we have almost 14 million pairs for training. First we need to make the dataset. The ’s are clear, we only need to rescale black and white’s strength. For ’s we need to define and extract data planes from the games, here I used the following 13 planes:
plane[0] = num_our_liberties == 1
plane[1] = num_our_liberties == 2
plane[2] = num_our_liberties == 3
plane[3] = num_our_liberties >= 4
plane[4] = num_enemy_liberties == 1
plane[5] = num_enemy_liberties == 2
plane[6] = num_enemy_liberties == 3
plane[7] = num_enemy_liberties >= 4
plane[8] = empty_points_on_board
plane[9] = history_played_before == 1
plane[10] = history_played_before == 2
plane[11] = history_played_before == 3
plane[12] = history_played_before == 4This is almost the source code in a tool I made (below). Basically the right sides are numpy arrays with some simple domain knowledge (for instance, planes 9 to 12 list the last 4 moves). The planes are basically a simple extension of the Clark, Storkey 2014 paper with the history moves and were proposed by Detlef Schmicker.
I used my github project deep-go-wrap which has a tool for making HDF5 datasets from Go game records and all the planes necessary. Making a dataset is as hard as running:
cat game_filenames | sort -R | ./make_dataset.py -l ranks -p detlef out.hdfNetwork
Now, the network. Since this is more like a proof-of-concept experiment, I went with a fairly simple network to have fast training. I used a few convolutions with a small dropout dense layer atop and 2 output neurons for strengths of the players.
- convolutional layer 128 times 5x5 filters, ReLU activation
- convolutional layer 64 times 3x3 filters, ReLU activation
- convolutional layer 32 times 3x3 filters, ReLU activation
- convolutional layer 8 times 3x3 filters, ReLU activation
- dense layer with 64 neurons, ReLU activation, 0.5 dropout
- 2 output neurons, linear activation
I used the keras.io library for implementation of the model, which can be found here. The network was trained for just 2 epochs with Adam optimizer, because it converged pretty quickly. I have a bigger network in training (using RMSProp), but it will take some time, so let’s have a look on results in the meantime ;-)
Results
Basically, we now have a network which predicts strength of both players from a single position (plus history of 4 last moves). This would be really cool if it worked, as we’ve previously recommended at least a sample of 10 games in our GoStyle webapp to predict strength somewhat reliably.
So, how good this really simple first-shot network — trained for quite a short time, without any fine-tuning — performs? And what would a good result be? Lets have a look on dependency of error (difference between wanted and predicted strength) on move number.
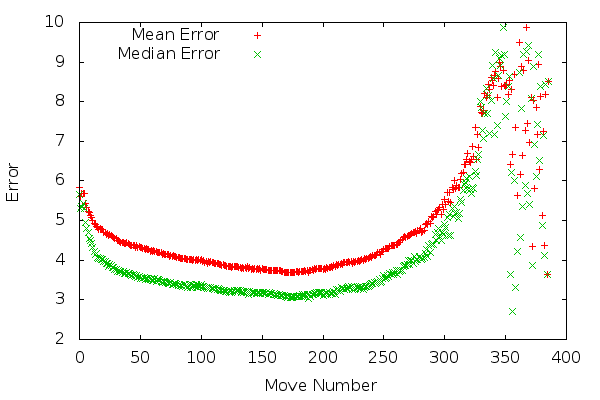
We can clearly see that the error is the highest at the beginning and end. Because games of beginners usually look the same to games of strong players at the beginning (first few moves are usually very similar) the first half of the statement is not really surprising. On the other hand, the fact that the error grows so steeply in the end is probably caused by the fact that there are only few very long games in the dataset (usual game takes about 250–300 moves). Before discussing whether these numbers are any good, let’s have a look on another graph, error by rank:
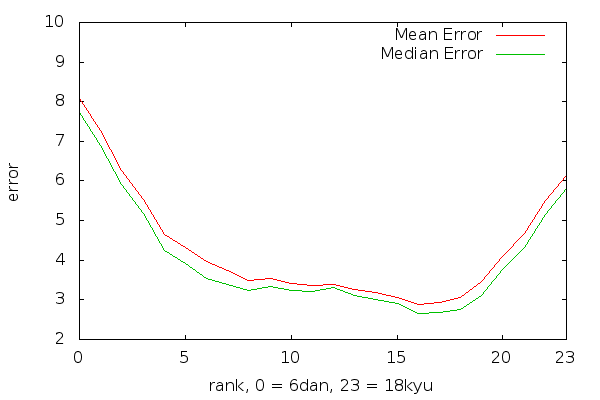
This graph basically shows that hardest ranks to be predicted correspond to both very strong and very weak players. A graph of a predictor which would always predict just the middle class would look like a letter “V” with the minimum in the middle. This graph has more of a “U” shape, which is good, because it means that the network is not only utilising statistical distribution of target ’s but also has some understanding of the data. Comparing with the naive V predictor is also interesting in terms of error. Were the 24 values of distributed uniformly randomly, the standard deviation of the always-the-middle V predictor would be `
On average, the network has (root of mean square error) or 4.66. The has a nice property that (under certain assumptions) it is an estimate of the . So by comparing 4.66 and 6.93, we can say that the network actually does something useful. This is of course a mediocre comparison and one would hope for the network to be much better than the simplest possible reference.
Comparison With Prior Work
In my recent paper Evaluating Go game records for prediction of player attributes, different features were extracted from games (samples of 10–40 them) and given a good predictive model, it was possible to predict the strength with the following :
- 2.788 Pattern feature
- 5.765 Local sequences
- 5.818 Border distance
- 5.904 Captured stones
- 6.792 Win/Loss statistics
- 5.116 Win/Loss points
The results in the paper had a slightly bigger domain of 26 ranks instead of 24, but roughly the numbers are still comparable. So 4.66 our brave new simplistic deep network has is better than all but the dominating feature (extracted from at least 10 games), and this from just one game position with history of size 4. Given that average game in the dataset is about 190 moves long, 10 games is 380 times more information than the network has.
Cool indeed!
What next?
- You have some ideas? I do. Stay tuned!